Tech companies are infamous for torturing career hopefuls with mind-melters during interviews. This week, you’ll try your hand at one without the stress of job prospects on your shoulders. Google is rumored to have used this puzzle over the years, although it has since retired the practice altogether.
I encountered this puzzle a long time ago, and it sounded to me like it would be tedious, so I didn’t give it much thought. Recently, I decided to roll up my sleeves and give it an honest try. I was pleasantly surprised to find it approachable and enjoyable to solve. I shouldn’t have been a neigh-sayer.
Did you miss last week’s puzzle? Check it out hereand find its solution at the bottom of today’s article. Be careful not to read too far ahead if you haven’t solved last week’s yet!
Puzzle #26: Horsing Around
A stable has 25 horses. You can race five horses of your choice at a time and learn who won, who came in second, etc.. You don’t learn how fast they ran, only what place the five horses got relative to each other. What is the minimum number of races you’ll need to identify the three fastest horses of the 25?
You don’t need to know the rank-order among the top three. You may assume that if you race the same horse twice, it will take the same amount of time to complete the track. There are also no ties.
If you’re feeling stuck, just picture a tech executive tossing your résumé in the bin.
I’ll be back next Monday with the answer and a new puzzle. Do you know a cool puzzle that you think should be featured here? Message me on Twitter @JackPMurtagh or email me at gizmodopuzzle@gmail.com
Solution to Puzzle #25: Chess Puzzles
Shout-out to Eugene for crushing all three of last week’s chess puzzles like a grandmaster. Puzzle one asked you to place five queens on a five-by-five board such that three squares were not attacked by any queen.
One insight that helped me solve this puzzle: Placing five queens to leave three squares unattacked is the same as placing three queens and leaving five squares unattacked. Either way, we’re finding a set of three squares and a set of five squares that don’t “see” each other by a queen’s move. Maneuvering only three queens made the trial and error much more manageable.

The black pawns are all safe. Rotations and reflections of this diagram are also valid solutions.
Puzzle two asked how many knights you could fit on a chess board without any of them attacking each other. The insight here is that knights only attack squares of the opposite color from the one they’re on. So you can put a knight on every square of the same color, for a total of 32 knights.
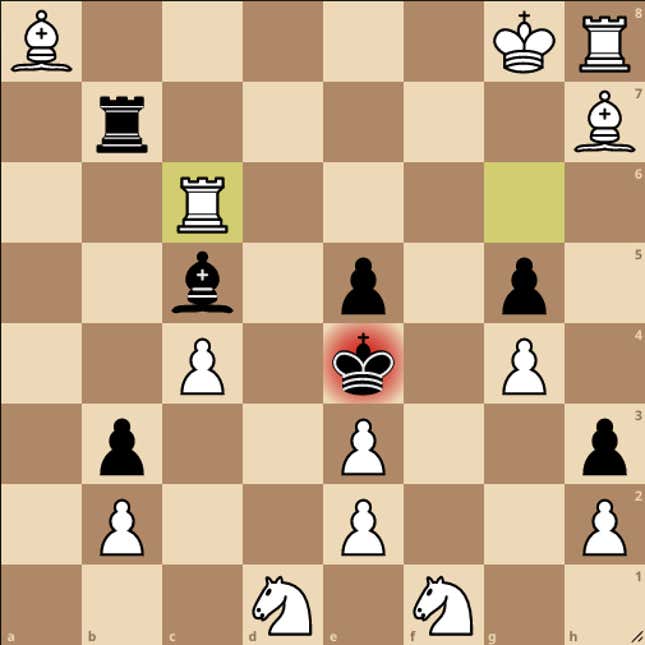
Finally, I gave you a whimsical puzzle by Karl Fabel asking you to find a move for white that does NOT cause instant checkmate in the position below.
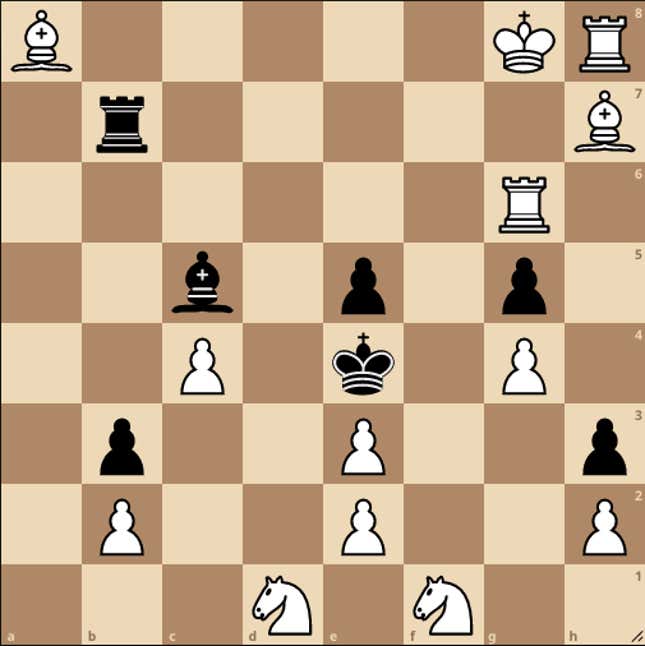
The solution is rook to c6 as depicted below. This unveils a discovered check on black’s king from white’s bishop on h7, but black can delay mate by capturing the bishop with their rook. Normally, this capture wouldn’t be possible because black’s rook is pinned by white’s bishop on a8 (it’s illegal to make moves that put your own king in check). But by moving their rook to c6, white blocks this pin and frees the black rook to stop the mate.